همگرائی و واگرائی سری ها
عضوهای مجموعهای را در نظر میگیریم و آنها را با نظم مشخصی مرتب میکنیم. مرتب کردن عضوهای مجموعه با نظم و ترتیب معین مفهوم سریها را پایهگذاری میکند. در اینصورت اگر تعداد جملههای مرتب شده محدود باشد سری محدود و اگر نامحدود باشد سری را نامحدود گوییم. در هر دو صورت ضابطه مشخص برای نوشتن جملههای سری وجود دارد.
مجموع یک سری
درک مفهوم سریها آسان است، کافی است عده محدودی از عددها را با جمع کنیم. این کار برای سریهای نامحدود به این سادگی نیست. نخست باید یک سری از جمعکها را تشکیل دهیم. جمله اول جمعک اول، مجموع دو جمله اول را جمعک دوم و... مینامیم. برای روشن شدن مطلب بهتر است از نمادهایی مرتبط استفاده کنیم. فرض کنیم جمله را با 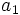 ، جمله دوم را با
، جمله دوم را با 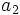 و جمله n ام سری را با
و جمله n ام سری را با  نمایش دهیم در اینصورت برای سری ذکر شده فوق خواهیم داشت:
نمایش دهیم در اینصورت برای سری ذکر شده فوق خواهیم داشت: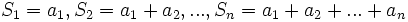
در عبارات بالا هر کدام از 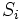 ها را که
ها را که  ، جمعک مینامیم. اگر سری نامحدود مجموعی داشته باشد. این مجموع حد
، جمعک مینامیم. اگر سری نامحدود مجموعی داشته باشد. این مجموع حد  است به ازای
است به ازای  این حد را S مینامیم. هر اندازه که n بزرگ باشد
این حد را S مینامیم. هر اندازه که n بزرگ باشد  باهم تفاوت دارند. این تفاوت را میتوانیم به اندازه دلخواه کوچک کنیم. در واقع هر چه تعداد جملههایی که در نظر میگیریم بیشتر باشد به مجموع سری نزدیکتر میشویم.
باهم تفاوت دارند. این تفاوت را میتوانیم به اندازه دلخواه کوچک کنیم. در واقع هر چه تعداد جملههایی که در نظر میگیریم بیشتر باشد به مجموع سری نزدیکتر میشویم.
همگرایی و واگرایی سریها
سری همگرا
اگر سری نامحدود مجموعی داشته باشد یعنی حد  به ازای
به ازای  وجود داشته باشد سری را همگرا مینامیم.
وجود داشته باشد سری را همگرا مینامیم.
سری واگرا
اگر  یا
یا 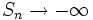 سری را واگرا مینامیم. مثالی ساده برای سری واگرا سریی است که همه جملههای آن یک باشد. مجموع این سری عبارت است از:....+1+1+1
سری را واگرا مینامیم. مثالی ساده برای سری واگرا سریی است که همه جملههای آن یک باشد. مجموع این سری عبارت است از:....+1+1+1
میبینیم که با انتخاب جملههای بیشتر میتوانیم این مجموع را به اندازه دلخواه بزرگ کنیم. در واقع میتوان چنین نتیجه گرفت که سریهای همگرا بعد از تعدادی مقادیر، به یک عددی نزدیک میشوند و حد جملهاش به یک عدد حقیقی میل میکند.
سری نوسانی
برخی از سریهای نامحدود نه همگرا هستند نه واگرا این سریها را سریهای نوسانی مینامیم. مثل...-1+1-1+1-1
در این سری داریم: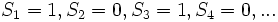
یعنی جمعکها بطوری تناوبی صفر و یک میشوند و  به ازای
به ازای  بسوی حد میل نمیکند. از طرفی مجموع این سری نمیتواند بیشتر از یک و یا کمتر از صفر باشد، بنابراین
بسوی حد میل نمیکند. از طرفی مجموع این سری نمیتواند بیشتر از یک و یا کمتر از صفر باشد، بنابراین  به
به 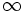 و
و  نیز میل نمیکند پس این سری نه همگرا است نه واگرا اگر فرمولی کلی برای مجموع اولین
نیز میل نمیکند پس این سری نه همگرا است نه واگرا اگر فرمولی کلی برای مجموع اولین  جمله سری وجود نداشته باشد همگرایی سری را نمیتوان مستقیما بنابر تعریف آزمایش کرد. ولی تشخیص همگرایی و واگرایی یک سری بیش از یافتن مجموع سری در حالت همگرایی اهمیت دارد.
جمله سری وجود نداشته باشد همگرایی سری را نمیتوان مستقیما بنابر تعریف آزمایش کرد. ولی تشخیص همگرایی و واگرایی یک سری بیش از یافتن مجموع سری در حالت همگرایی اهمیت دارد.
سخن آخر
بطور کلی از همگرایی میتوان اینگونه تعبیری داشت که برای سریها یا دنبالههای همگرا بعد از مدتی تمامی جملهها به یک مقدار معین و منحصر به فردی نزدیک میشوند که در آن نقطه میتوان رفتار سری را بررسی کرد. یا اینکه در نقطه همگرایی جملات با هم متحد و یگانه میشوند. در صورتی که در سریهای واگرا و همینطور دنبالههای واگرا هرگز چنین اتفاقی نمیافتد و جملات در یک ویژگی خاص صدق نمیکنند مثل توابع متناوب که در بالا اشاره شد هر کدام برای مقادیر مختلف، جوابهای متفاوتی را به ما میدهند و ما هرگز نمیتوانیم آنها را در تعداد بینهایت جمله به یک مقدار حقیقی و ثابت نسبت دهیم یا متحد سازیم.
- لینک منبع
تاریخ: دوشنبه , 02 مرداد 1402 (03:44)
- گزارش تخلف مطلب
